dsac::graph Namespace Reference

Code from the chapter "Graph Algorithms". More...

Data Structures
class	Graph
class	Partition

Typedefs
template<typename V , typename E >
using	VertexList = std::list< typename Graph< V, E >::Vertex >
	VertexList is a std::list of Vertex instances for Graph<V,E>
template<typename V , typename E >
using	EdgeList = std::list< typename Graph< V, E >::Edge >
	EdgeList is a std::list of Edge instances for Graph<V,E>
template<typename V , typename E >
using	VertexSet = std::unordered_set< typename Graph< V, E >::Vertex, typename Graph< V, E >::VertexHash >
	VertexSet is a std::unordered_set of Vertex instances for Graph<V,E>
template<typename V , typename E , typename T >
using	VertexMap = std::unordered_map< typename Graph< V, E >::Vertex, T, typename Graph< V, E >::VertexHash >
	VertexMap is a std::unordered_map from Vertex to type T for Graph<V,E>
template<typename V , typename E >
using	VertexIntMap = VertexMap< V, E, int >
	VertexIntMap is a std::unordered_map from Vertex to int for Graph<V,E>
template<typename V , typename E >
using	VertexVertexMap = VertexMap< V, E, typename Graph< V, E >::Vertex >
	VertexVertexMap is a std::unordered_map from Vertex to Vertex for Graph<V,E>
template<typename V , typename E >
using	VertexEdge = VertexMap< V, E, typename Graph< V, E >::Edge >
	VertexEdgeMap is a std::unordered_map from Vertex to Edge for Graph<V,E>

Functions
template<typename V , typename E >
void	dump (const Graph< V, E > &G, std::ostream &out)
	Outputs graph representation to given stream.
template<typename V , typename E >
Graph< V, E >	graph_from_edgelist (std::list< std::tuple< V, V, E, int > > edgelist, bool is_directed=false)
Graph< std::string, std::string >	figure_14_1_2 ()
	Returns the unweighted, directed graph from Figure 14.1.2 of DSAC.
Graph< std::string, std::string >	figure_14_1_3 ()
	Returns the unweighted, directed graph from Figure 14.1.3 of DSAC.
Graph< std::string, std::string >	figure_14_4_1 ()
	Returns the unweighted, directed graph from Figure 14.4.1 of DSAC.
Graph< std::string, std::string >	figure_14_4_2 ()
	Returns the unweighted, undirected graph from Figure 14.4.2 of DSAC.
Graph< std::string, std::string >	figure_14_4_3 ()
Graph< std::string, std::string >	figure_14_5_1 ()
	Returns the unweighted, directed graph from Figure 14.5.1 of DSAC.
Graph< std::string, std::string >	figure_14_6_1 ()
	Returns the unweighted, directed graph from Figure 14.6.1 of DSAC.
Graph< std::string, std::string >	figure_14_6_2 ()
Graph< std::string, std::string >	figure_14_7_1 ()
	Returns the unweighted, undirected graph from Figure 14.7.1 of DSAC.
Graph< std::string, std::string >	figure_14_7_2 ()
	Returns the unweighted, undirected graph from Figure 14.7.2 of DSAC.
Graph< std::string, std::string >	figure_14_8_2 ()
Graph< std::string, std::string >	figure_14_8_3 ()
template<typename V , typename E >
EdgeList< V, E >	mst_prim_jarnik (const Graph< V, E > &g)
template<typename V , typename E >
EdgeList< V, E >	mst_kruskal (const Graph< V, E > &g)
template<typename V , typename E >
VertexIntMap< V, E >	shortest_path_distances (const Graph< V, E > &g, typename Graph< V, E >::Vertex src)
template<typename V , typename E >
VertexVertexMap< V, E >	shortest_path_tree (const Graph< V, E > &g, typename Graph< V, E >::Vertex src, const VertexIntMap< V, E > &D)
template<typename V , typename E >
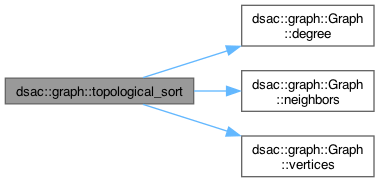
VertexList< V, E >	topological_sort (const Graph< V, E > &g)
template<typename V , typename E >
Graph< V, E >	floyd_warshall (const Graph< V, E > &g)
	Returns a new graph that is the transitive closure of g.
template<typename V , typename E >
void	dfs (const Graph< V, E > &g, typename Graph< V, E >::Vertex u, VertexVertexMap< V, E > &discovered)
template<typename V , typename E >
VertexVertexMap< V, E >	dfs_complete (const Graph< V, E > &g)
	Performs DFS of an entire graph, returning the discovery map.
template<typename V , typename E >
void	bfs (const Graph< V, E > &g, typename Graph< V, E >::Vertex s, VertexVertexMap< V, E > &discovered)
template<typename V , typename E >
VertexList< V, E >	construct_path (const Graph< V, E > &g, typename Graph< V, E >::Vertex u, typename Graph< V, E >::Vertex v, const VertexVertexMap< V, E > &discovered)

Detailed Description

Code from the chapter "Graph Algorithms".

Typedef Documentation

EdgeList

template<typename V , typename E >

using dsac::graph::EdgeList = typedef std::list<typename Graph<V,E>::Edge>

EdgeList is a std::list of Edge instances for Graph<V,E>

VertexEdge

template<typename V , typename E >

using dsac::graph::VertexEdge = typedef VertexMap<V,E,typename Graph<V,E>::Edge>

VertexEdgeMap is a std::unordered_map from Vertex to Edge for Graph<V,E>

VertexIntMap

template<typename V , typename E >

using dsac::graph::VertexIntMap = typedef VertexMap<V,E,int>

VertexIntMap is a std::unordered_map from Vertex to int for Graph<V,E>

VertexList

template<typename V , typename E >

using dsac::graph::VertexList = typedef std::list<typename Graph<V,E>::Vertex>

VertexList is a std::list of Vertex instances for Graph<V,E>

VertexMap

template<typename V , typename E , typename T >

using dsac::graph::VertexMap = typedef std::unordered_map<typename Graph<V,E>::Vertex, T, typename Graph<V,E>::VertexHash>

VertexMap is a std::unordered_map from Vertex to type T for Graph<V,E>

VertexSet

template<typename V , typename E >

using dsac::graph::VertexSet = typedef std::unordered_set<typename Graph<V,E>::Vertex, typename Graph<V,E>::VertexHash>

VertexSet is a std::unordered_set of Vertex instances for Graph<V,E>

VertexVertexMap

template<typename V , typename E >

using dsac::graph::VertexVertexMap = typedef VertexMap<V,E,typename Graph<V,E>::Vertex>

VertexVertexMap is a std::unordered_map from Vertex to Vertex for Graph<V,E>

Function Documentation

bfs()

template<typename V , typename E >

void dsac::graph::bfs	(	const Graph< V, E > &	g,
		typename Graph< V, E >::Vertex	s,
		VertexVertexMap< V, E > &	discovered
	)

Performs BFS of the undiscovered portion of Graph g starting at Vertex s

discovered maps each vertex to the discovery vertex used to reach it in DFS root of a search tree is canonically marked with itself as the discovery vertex

Here is the call graph for this function:

construct_path()

template<typename V , typename E >

VertexList< V, E > dsac::graph::construct_path	(	const Graph< V, E > &	g,
		typename Graph< V, E >::Vertex	u,
		typename Graph< V, E >::Vertex	v,
		const VertexVertexMap< V, E > &	discovered
	)

Returns list of vertices on directed path from u to v (or empty list if v not reachable) based upon the discovery map from a previous graph traversal

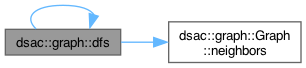
dfs()

template<typename V , typename E >

void dsac::graph::dfs	(	const Graph< V, E > &	g,
		typename Graph< V, E >::Vertex	u,
		VertexVertexMap< V, E > &	discovered
	)

Performs DFS of the undiscovered portion of Graph g starting at Vertex u

discovered maps each vertex to the discovery vertex used to reach it in DFS root of a search tree is canonically marked with itself as the discovery vertex

Here is the call graph for this function:

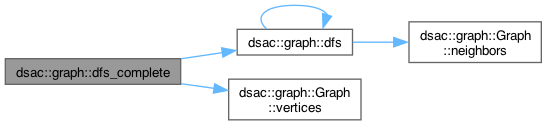
dfs_complete()

template<typename V , typename E >

VertexVertexMap< V, E > dsac::graph::dfs_complete

(

const Graph< V, E > &

g

)

Performs DFS of an entire graph, returning the discovery map.

Here is the call graph for this function:

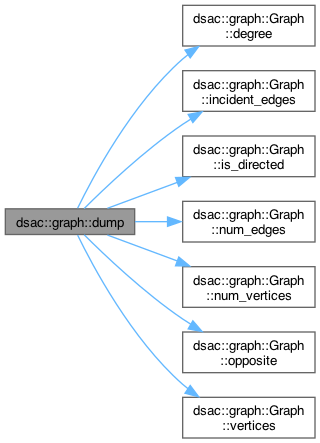
dump()

template<typename V , typename E >

void dsac::graph::dump	(	const Graph< V, E > &	G,
		std::ostream &	out
	)

Outputs graph representation to given stream.

Here is the call graph for this function:

figure_14_1_2()

Graph< std::string, std::string > dsac::graph::figure_14_1_2

(

)

Returns the unweighted, directed graph from Figure 14.1.2 of DSAC.

Here is the call graph for this function:

figure_14_1_3()

Graph< std::string, std::string > dsac::graph::figure_14_1_3

(

)

Returns the unweighted, directed graph from Figure 14.1.3 of DSAC.

Here is the call graph for this function:

figure_14_4_1()

Graph< std::string, std::string > dsac::graph::figure_14_4_1

(

)

Returns the unweighted, directed graph from Figure 14.4.1 of DSAC.

Here is the call graph for this function:

figure_14_4_2()

Graph< std::string, std::string > dsac::graph::figure_14_4_2

(

)

Returns the unweighted, undirected graph from Figure 14.4.2 of DSAC.

Here is the call graph for this function:

figure_14_4_3()

Graph< std::string, std::string > dsac::graph::figure_14_4_3

(

)

Returns the unweighted, undirected graph from Figure 14.4.3 of DSAC (same as Figure 14.4.2)

Here is the call graph for this function:

figure_14_5_1()

Graph< std::string, std::string > dsac::graph::figure_14_5_1

(

)

Returns the unweighted, directed graph from Figure 14.5.1 of DSAC.

Here is the call graph for this function:

figure_14_6_1()

Graph< std::string, std::string > dsac::graph::figure_14_6_1

(

)

Returns the unweighted, directed graph from Figure 14.6.1 of DSAC.

Here is the call graph for this function:

figure_14_6_2()

Graph< std::string, std::string > dsac::graph::figure_14_6_2

(

)

Returns the unweighted, directed graph from Figure 14.6.2 of DSAC (same as Figure 14.6.1)

Here is the call graph for this function:

figure_14_7_1()

Graph< std::string, std::string > dsac::graph::figure_14_7_1

(

)

Returns the unweighted, undirected graph from Figure 14.7.1 of DSAC.

Here is the call graph for this function:

figure_14_7_2()

Graph< std::string, std::string > dsac::graph::figure_14_7_2

(

)

Returns the unweighted, undirected graph from Figure 14.7.2 of DSAC.

Here is the call graph for this function:

figure_14_8_2()

Graph< std::string, std::string > dsac::graph::figure_14_8_2

(

)

Returns the unweighted, undirected graph from Figure 14.8.2 of DSAC (same as Figure 14.7.2)

Here is the call graph for this function:

figure_14_8_3()

Graph< std::string, std::string > dsac::graph::figure_14_8_3

(

)

Returns the unweighted, undirected graph from Figure 14.8.3 of DSAC (same as Figure 14.7.2 and 14.8.2)

Here is the call graph for this function:

floyd_warshall()

template<typename V , typename E >

Graph< V, E > dsac::graph::floyd_warshall

(

const Graph< V, E > &

g

)

Returns a new graph that is the transitive closure of g.

Here is the call graph for this function:

graph_from_edgelist()

template<typename V , typename E >

Graph< V, E > dsac::graph::graph_from_edgelist	(	std::list< std::tuple< V, V, E, int > >	edgelist,
		bool	is_directed = false
	)

Here is the call graph for this function:

mst_kruskal()

template<typename V , typename E >

EdgeList< V, E > dsac::graph::mst_kruskal

(

const Graph< V, E > &

g

)

Computes a minimum spanning tree of graph g with Kruskal's algorithm

Graph should be connected and have nonnegative edge weights.

Here is the call graph for this function:

mst_prim_jarnik()

template<typename V , typename E >

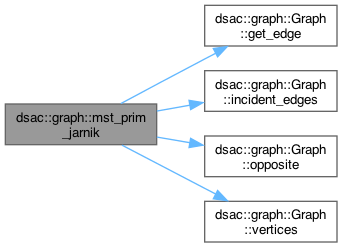
EdgeList< V, E > dsac::graph::mst_prim_jarnik

(

const Graph< V, E > &

g

)

Computes a minimum spanning tree of graph g with the Prim-Jarnik algorithm

Graph should be connected and have nonnegative edge weights.

Here is the call graph for this function:

shortest_path_distances()

template<typename V , typename E >

VertexIntMap< V, E > dsac::graph::shortest_path_distances	(	const Graph< V, E > &	g,
		typename Graph< V, E >::Vertex	src
	)

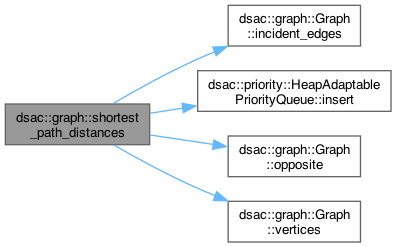
Computes shortest-path distances from src to reachable vertices of g.

Graph can be undirected or directed but must have nonnegative edge weights

Here is the call graph for this function:

shortest_path_tree()

template<typename V , typename E >

VertexVertexMap< V, E > dsac::graph::shortest_path_tree	(	const Graph< V, E > &	g,
		typename Graph< V, E >::Vertex	src,
		const VertexIntMap< V, E > &	D
	)

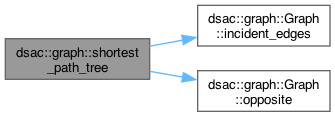
reconstructs shortest-path tree rooted at vertex src, given computed distance map D Each vertex is mapped to its parent vertex in the tree (with src mapped to itself)

Here is the call graph for this function:

topological_sort()

template<typename V , typename E >

VertexList< V, E > dsac::graph::topological_sort

(

const Graph< V, E > &

g

)

Returns a list of vertices of graph g in topological order If no order is possible, the result will have less than n vertices

Here is the call graph for this function: